Many simulations or experiments in the field of granular materials are perform with two spatial dimensions, using cylinders instead of actual grains. This allows to simplify the problem and reduce the number of grains considered. However, there are some difference between two-dimensional grains and three-dimensional ones.
This project pushes the question forward: what would happened if higher dimensional grains were considered? Like a flow of four-dimensional or five dimensional (hyper)spheres. As this is not achievable experimentally (after all, we only have three dimensions of space), we developed a numerical simulation tool to study just this: NDDEM.
Here is for example an inlined plane flow of three-, four-, and five- dimensional monodisperse hyperspheres (all the grains are the same size, they appear different sizes on screen due to their distance in the non-visible dimensions):
More advance descriptions and videos explaining these concepts are available here.
NDDEM is actually a full-fleshed discrete element solver that works in any number of spatial dimensions. It includes
- Discrete element solver of hypersphere with translational and rotational degrees of freedom, elastic and frictional contact laws, polydisperse particles, periodic boundary conditions in any dimension, Lees-Edward boundary conditions.
- Coarse-graining solver with Lucy function in any number of spatial dimensions
- Texturing of rotating hyperspheres in any number of spatial dimensions.
This allowed to perform some mechanical tests in higher dimension frictional granular materials:
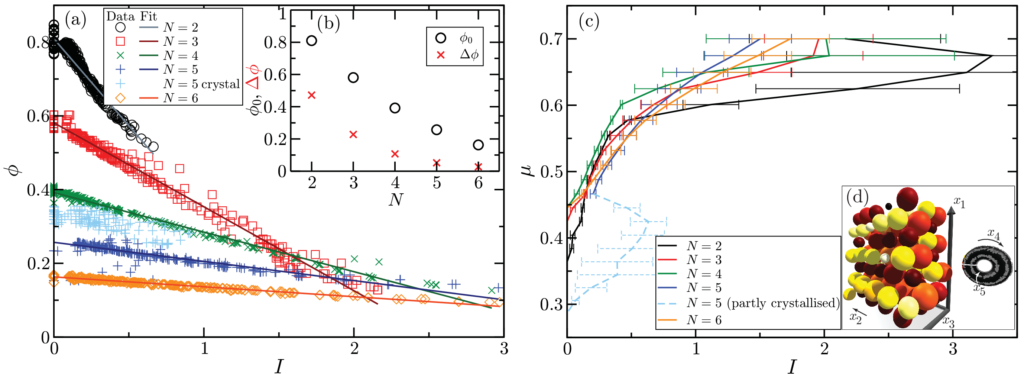
number I for various dimensions N. (b) Values of best linear fit parameters to φ = φ0 − φI as a function of N. (c) Friction coefficient μ as a
function of inertial number I. The measured I is averaged across the depth of the flow from the local coarse-grained values, and the error bars are the standard deviation around this mean estimation and do not take into account the uncertainty in the coarse-graining estimation (decreasing with increasing N). There are ∼15 coarse-graining points in the flowing layer along e1 , using a window size w = 3r; see Appendix C for more details. (d) Example of a 5D crystalline state [shown in light blue in (a) and (c)]. Particle coloring indicates the location of the particle center in x5 . Particle centers in x4 and x5 are depicted on the torus in gray
Resources:
[Download] Guillard, François, and Benjy Marks. “Frictional hyperspheres in hyperspace.” Physical Review E 103.5 (2021): 052901.
Additional explanations and resources for NDDEM
This page contain several teaching resources based on the 2D or 3D version of NDDEM.